Generación de muestras para un Noise Conditional Score Networks (NCSNs). Paper: Generative Modeling by Estimating Gradients of the Data Distribution.

En algunos casos, los modelos probabilísticos en Machine Learning vienen en forma de una densidad de probabilidad (p.d.f.) no normalizada. Es decir, esta función describe la forma de la distribución, pero no garantiza que el área total bajo la curva sea igual a uno.

Supongamos que se tiene un vector aleatorio $x\in\mathbb{R}^n$ el cual sigue una distribución no-normalizada $q(x)$. Esta densidad puede convertirse en una distribución válida al dividirla por una constante de normalización $Z$:

\[p_{\text{data}}(x) = \frac{1}{Z}q(x),\]

donde $Z=\int q(x)dx$ y $\int p_{\text{data}}(x)dx=1$. El cálculo de esta constante puede ser analíticamente intratable, debido a la alta dimensionalidad del espacio de datos. Por ese motivo, existen métodos para estimar funciones de densidad no normalizadas, uno de los cuales se basa en el cálculo del Score.

El Score es el gradiente de la densidad logarítmica con respecto a la variable aleatoria $x$:

\[\nabla_x \log p_{\text{data}}(x).\]

En el caso de un modelo generativo basado en el Score. El objetivo principal es entrenar una red neuronal $s_{\theta}(x)$ para predecir directamente $\nabla_x \log p_{\text{data}}(x)$, en lugar de $p_{\text{data}}(x)$. Luego, esta predicción puede ser utilizada para generar muestras sintéticas utilizando la ecuación de Langevin—un método estocástico utilizado en la física para simular el movimiento de partículas.

Noise Conditional Score Networks (NCSNs)

En la práctica los datos no están distribuidos uniformemente en el espacio de datos $\mathbb{R}^n$, sino que están concentrados en una región de menor dimensión.

Esto significa que el Score de la distribución de datos estaría indefinido en la mayoría de los puntos del espacio. Una solución a este problema es perturbar los datos con ruido gaussiano. Dado que el soporte del ruido gaussiano es todo el espacio, el Score de la distribución de datos perturbados estará definido para todos los puntos. Además, al agregar ruido, se puede rellenar regiones del espacio con baja densidad de probabilidad en la distribución de datos original. Esto permite que el Score de la distribución de datos perturbados sea más fácil de estimar, dado que van a existir más puntos en estas regiones.

Para este propósito definimos $(\sigma_i)^L_{i=1}$ como una secuencia geométrica positiva la cual se rige de la siguiente manera:

\[\frac{\sigma_1}{\sigma_2}=\cdots=\frac{\sigma_{L-1}}{\sigma_L}>1.\]

El objetivo es ahora entrenar una red neuronal que estime el Score de todos los datos perturbados $\tilde{x}$. Es decir $\forall \sigma\in (\sigma_i)^L_{i=1}:s_{\theta}(\tilde{x},\sigma)\approx $ $\nabla_{\tilde{x}} \log q_{\sigma}(\tilde{x}|x)$. Donde $q_{\sigma}(\tilde{x}|x)=\mathcal{N}(\tilde{x}|x,\sigma^2I)$. Sin embargo, ¿Cómo llegamos a predecir $\nabla_x \log p_{\text{data}}(x)$ a partir de $s_{\theta}(\tilde{x},\sigma)$?

Bueno, la respuesta a esta pregunta se resuelve con una identidad fácilmente demostrable:

\(\mathbb{E}_{q_{\sigma}(\tilde{x},x)} \left[ \left\| s_{\theta}(\tilde{x}, \sigma) - \nabla_{\tilde{x}} \log q_{\sigma}(\tilde{x}|x) \right\|^2_2 \right]=\mathbb{E}_{q_{\sigma}(\tilde{x})} \left[ \left\| s_{\theta}(\tilde{x}, \sigma) - \nabla_{\tilde{x}} \log q_{\sigma}(\tilde{x}) \right\|^2_2 \right],\)

donde para un valor óptimo de $\theta={\theta}^*$ y un $\sigma$ lo suficientemente pequeño se cumple que:

\[s_{\theta}(x)=\nabla_x \log q_{\sigma}(x)\approx \nabla_x \log p_{\text{data}}(x).\]

Ahora que sabemos como estimar el Score de la distribución de datos, podemos simplificar el primer término en la equivalencia anterior. Dando como resultado la siguiente función de pérdida:

\[\mathcal{L}(\theta;\sigma) = \frac{1}{2}\mathbb{E}_{p_{\text{data}}(x)} \mathbb{E}_{\tilde{x}\sim \mathcal{N}(x,\sigma^2I)} \left[ \left\| s_{\theta}(\tilde{x}, \sigma) + \frac{(\tilde{x}-x)}{\sigma^2} \right\|^2_2 \right]\]

Al final, la función de pérdida se pondera para todos los valores de $\sigma_i$.

El algoritmo de muestreo

Una vez que la red neuronal ha sido entrenada y tenemos una aproximación del Score de la distribución de datos $s_{\theta}(x)\approx \nabla_x \log p_{\text{data}}(x)$, podemos empezar a generar muestras sintéticas. Para ello, dado un $\epsilon>0$, y un valor inicial $x_0\sim \mathcal{N}(0,I)$, el algoritmo de muestreo se define bajo la siguiente ecuación:

\[x_{i} = x_{i-1} + \epsilon s_{\theta}(x_{i-1}) + \sqrt{2\epsilon}z_{i-1}, i=1,\ldots,T,\]

donde $z_{i-1}\sim \mathcal{N}(0,I)$ y la distribución de $x_T$ converge a una muestra de la distribución de los datos de entrenamiento cuando $\epsilon\rightarrow 0$ y $T\rightarrow \infty$.

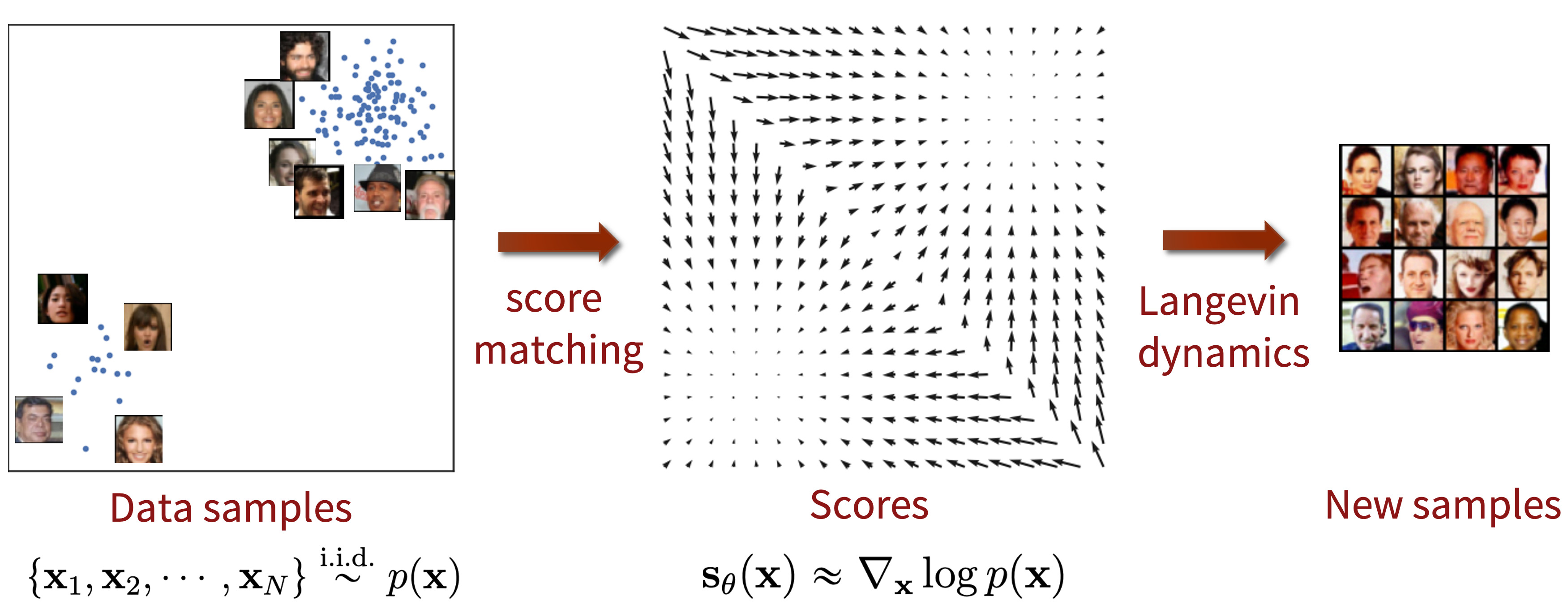
Score Based Generative Models. Imagen importada de yang-song.net.

Este método de muestreo es conocido como Langevin Dynamics, una técnica para simular el movimiento de partículas diriga por fuerzas aleatorias y deterministas. En este caso, la red neuronal $s_{\theta}(x)$ actúa como el término determinista, como una “fuerza” que guía la trayectoria para generar una muestra realista. Mientras que $z_t$ introduce aleatoriedad, asegurando la diversidad en las muestras generadas.

Intuitivamente, el score $\nabla_x \log p_{\text{data}}(x)$ empuja a $x_{i-1}$ hacia regiones de alta probabilidad en el espacio de datos. Cuando $p_{\text{data}}(x)$ es pequeño, el Score tiene un modulo grande, lo que significa que $x_{i-1}$ se aleja de estas regiones. Conforme $p_{\text{data}}(x)$ aumenta, el módulo del Score disminuye, lo que hace que $x_{i-1}$ se acerque poco a poco a estas regiones. En otras palabras, el Score asegura el movimiento hacia regiones de alta probabilidad—hacia muestras más realistas.